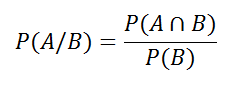En distintos momentos de nuestra educación tenemos algunos roces con la probabilidad. Desde edades muy tempranas empezamos a formar nuestras nociones de justo e injusto y parece que acordamos que las maneras justas de tomar decisiones pasan por el azar: lanzar una moneda, jugar disparejo o piedra, papel, tijera.
En la escuela aprendemos sobre la probabilidad clásica teniendo mucho cuidado de meter bajo la alfombra la difícil discusión sobre su circularidad: para definir la probabilidad de eventos sencillos asumimos su equiprobabilidad, dejándole las respectivas demostraciones al lector.
Más adelante hablamos con mucha naturalidad sobre la probabilidad de eventos aleatorios extremadamente complejos y decimos, con seguridad, que "Hay un 76% de probabilidad de lluvia" o que "Los Delfines de Miami tienen menos de 1% de probabilidad de ganar".
Quienes tenemos algo de oportunidad, el siguiente paso hacia adelante se llama Probabilidad Condicional: calcular la probabilidad de un evento suponiendo que ha pasado alguno otro. Esto se define de la siguiente manera,
y se lee: "La probabilidad de A dado B es igual a la probabilidad de A y B, dividido entre la probabilidad de B".
Hagamos aquí un ejemplo: Vas a elegir una carta de la bajara inglesa de 52 naipes. Si alguien más recibirá una carta primero, ¿cuál es la probabilidad de sacar el 7 de diamantes?
Puesto que no sabemos cuál fue la carta que recibió la primera persona, debemos hacer dos casos disjuntos y sumarlos: si ya salió el 7 de diamantes, si no ha salido aún. Sin embargo, si ya ha salido, la probabilidad de sacarlo es 0. Si no ha salido, la probabilidad es 1/51 dividido entre 51/52. Simplificando, la probabilidad es 1/52.
Es decir: si no sabes que carta ha salido todavía, la probabilidad de sacar la carta que quieres es la misma y creo que eso es hermoso.