¿Cuántas maneras conoces para calcular el área de un triángulo? ¿Dos, tres? Si nada más te sabes una y tus amigos se burlan de ti por eso, esta entrada es para ti (además, necesitas nuevos amigos). Te presentamos seis fórmulas para el área de un triángulo; si te sabes una distinta de éstas, por favor compártela con nosotros.
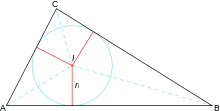
1. Base por altura (sobre dos)
Esta fórmula nos la enseñan en la primaria y es, para muchos, la única forma que tienen para calcular el área de un triángulo. El razonamiento es bastante sencillo: cuando nos dan un triángulo cualquiera, podemos hacer una copia de él, girarlo y crear un paralelogramo. Si no estamos convencidos, podemos convertir ese paralelogramo en un rectángulo y ¡pum! base por altura. Como esa es el área de dos triángulos idénticos, el área de nuestro triángulo será la mitad.
(Para convencernos que el área de un rectángulo es base por altura, podemos dividir en cuadritos unitarios y contarlos. Creo que lo del cuadrito unitario no lo podría explicar más, aunque quisiera.)
Es importante destacar -porque hay a quienes se les olvida- que en el caso particular de un triángulo rectángulo, siempre podemos usar un cateto como la altura y el otro como la base. Además, que la altura la puedes trazar sobre cualquiera de los lados y no solo sobre el lado en el que se "acuesta" tu triángulo.
2. Herón
Para los y las participantes de Olimpiada, la segunda fórmula que se suelen aprender es la de Herón. Para usar esta fórmula, necesitamos conocer la medida de los lados que llamamos a, b, c. Calculamos el área como
donde s es el semiperímetro, es decir, la mitad del perímetro,
La demostración original de Herón utiliza cuadriláteros cíclicos, pero no la conocemos. Existen pruebas muy sencillas con trigonometría y hasta con Teorema de Pitágoras. Acá hay unas pruebas particularmente hermosas, en inglés y con determinantes.
3. ab sen(C)
La fórmula de Herón depende de la longitud de los tres lados, que es un criterio de congruencia (LLL). Otro criterio es dos lados y el ángulo entre ellos (LAL) y esta fórmula es cuando conoces esos datos.
Esta fórmula es fácil de derivar conociendo las definiciones elementales de trigonometría. En particular, sabiendo que el seno de un ángulo -en un triángulo rectángulo- es igual al cateto opuesto sobre la hipotenusa. Puede que nuestro triángulo ABC no siempre sea rectángulo pero eso se arregla trazando la altura que va a alguno de los lados que conocemos:
Desde el ángulo que conocemos, podemos expresar su seno como h/b, donde h es la longitud de la altura que acabamos de trazar. Despejando h de la expresión sin(C) = h/b, obtenemos h = b sin(C). Obtenemos la fórmula inmediatamente.
4. abc sobre 4 veces el circunradio
Esta fórmula se deriva directamente de la anterior y del Teorema del Seno, que dice
donde a, b, c son las longitudes de los lados opuestos a los ángulos A, B, C, respectivamente, en los vértices del triángulo ABC. Además, R es el radio de la circunferencia circunscrita al triángulo, es decir, la que pasa por los tres vértices.
En la fórmula anterior (3), usábamos sin (C). Con el Teorema del Seno, tenemos que c / sin (C) = 2R. Podemos despejar sin (C) = c 2R. Sustituyendo en la fórmula anterior, nos queda
que es nuestra cuarta fórmula.
5. semiperímetro por inradio
El inradio es el radio de la circunferencia inscrita al triángulo, es decir, la que es tangente a los tres lados por adentro del triángulo. Existen otras tres circunferencias, llamadas excírculos, que son tangentes a los tres lados del triángulo, pero por afuera.
Es sencillo ver de dónde viene esta fórmula: une el incentro con los vértices. Obtienes tres triángulos cuya base es uno de los lados y cuya altura es... ¡el inradio!
Usando repetidamente la fórmula de base por altura y sacando factor común obtenemos lo que queremos:
Existen varias fórmulas en función de los exradios, que no vimos aquí pero puedes consultar en esta liga. Si no te imaginas los excírculos, tenemos esta imagen para ti:
6. las medianas
Si eres olimpiquito, estamos seguros que las cinco fórmulas anteriores no te sorprenden. Sin embargo, estamos casi seguros que ésta sí: es posible calcular el área de un triángulo si conoces la longitud de las medianas. ¿Cómo? Bueno, no sabemos si lo sepas pero es posible formar un triángulo cuyos lados midan lo mismo que las tres medianas de un triángulo dado. Por si fuera poco, el área de ese triángulo es 3/4 del área del triángulo original.
Esta imagen puede servir como una prueba gráfica:
Ahora que sabes eso, el resto es sencillo: usa Herón. Es decir, si u, v, w son las longitudes de las medianas del triángulo, podemos calcular su área como
donde s es el semiperímetro como siempre (solo que en este caso es la mitad de u+v+w).
(Extra: 7. Las Agujetas de Gauss
Este algoritmo funciona para cualquier polígono en un plano coordenado. Cuando trabajas en Olimpiada, no es tan complicado meterle coordenadas a tus triángulos: siempre puedes poner el lado más largo sobre el eje x y el tercer vértice sobre el eje y; eso te deja tres ceros en tus coordenadas y tres incógnitas.
Vamos a explicar cómo va este algoritmo. Digamos que quieres calcular el área del triángulo que tiene vértices en (2, 4), (3, -8), (1, 2). Lo que tienes que hacer es lo siguiente: escribe las coordenadas en una lista -en una matriz, en realidad- poniendo las coordenadas x en una columna, las y en otra columna y repitiendo la última coordenada. Queda algo así:
En este caso, obtenemos 2x(-8) + 3x2 + 1x4 = -16 + 6 + 4 = -6.
Haces lo mismo con las diagonales hacia la izquierda.
En este caso, obtenemos 4x3 + (-8)x1 + 2x2 = 12 - 8 + 4 = 8.El área del triángulo es la mitad de la diferencia en valor absoluto. Es decir la mitad de |(-6) - 8| = 14. O sea que el área del triángulo es 7.)
Estamos preparando un video para platicar todas estas fórmulas. ¿Conoces alguna otra?

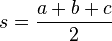


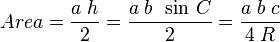



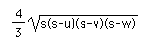

No hay comentarios.:
Publicar un comentario