Muchas de las matemáticas que se hacen empiezan por sencilla curiosidad. La Matemática puede entenderse como un conjunto de reglas con las que uno juega a ver qué sale, por lo que es natural jugar con ellas a ver qué sale. Otra manera muy popular de hacer matemáticas es usarla para contestar preguntas y una de esas grandes preguntas que ha intrigado a la humanidad durante siglos es la siguiente: ¿cómo dividir la pizza de manera justa?
Hay muchas matemáticas que puedes hacer con una pizza. Podemos empezar con el viejo chiste del volumen de una pizza: para una pizza de radio z y altura a, podemos calcular el volumen como π·(z^2)·a, o bien...
También, podemos hacer muchos problemas para saber qué pizza es mejor en relación tamaño/precio. Como la fórmula del área de un círculo eleva al cuadrado el radio, el área crece de manera cuadrática; si los precios crecen de manera lineal, entonces es mejor decisión la pizza más grande. Por ejemplo, si por una pizza del doble de radio te quieren cobrar el doble de precio, te están ofreciendo una ganga, pues el radio doble hace cuatro veces más pizza.
Al menos para ciertas condiciones. Claro que la gente que le pone precio a las pizzas en general sabe de esto y, bueno, tampoco es bueno para la dieta pedir la pizza más grande nada más porque es más barata.
Si le seguimos, podemos usar el Teorema de Pitágoras para jugar con la pizza. Como Pitágoras es una relación entre áreas (cuadrática), en general puedes extenderlo a casi cualquier tipo de figura, siempre que estés multiplicando por el mismo factor constante cada lado. Así, si el Teorema de Pitágoras se cumple para cuadrados, también se cumple para medios círculos, es decir, medias pizzas.
Si la relación a^2 + b^2 = c^2 se cumple, entonces también se cumple la relación para la mitad del cuadrado de la mitad, multiplicado por π. (Esto porque 1/2, 1/4 y π son todos factores constantes y están todos en cada uno de los sumandos.) Luego, en un arreglo como el de la figura, como el ángulo es mayor a 90º, la pizza grande tiene más área que las otras dos; en un ángulo exactamente de 90º, la pizza grande tiene la misma área que la chica y la mediana; en un ángulo menor a 90º, la pizza grande tiene menor área que las otras dos.
El teorema ahora sí
De todas las cosas realmente matemáticas que hemos hablado aquí, el Teorema de la Pizza es el más sencillo de enunciar e, incluso, de demostrar. Hablamos de cómo dividir una pizza en dos partes iguales. Por supuesto, podrás intentar hacerlo con un corte a la mitad, marcando un diámetro del círculo. Cortando la pizza en ocho pedazos de la manera tradicional, sabemos que si estos fueran iguales, basta con que cada uno tome cuatro de ellos. ¿Qué pasa si no son iguales?
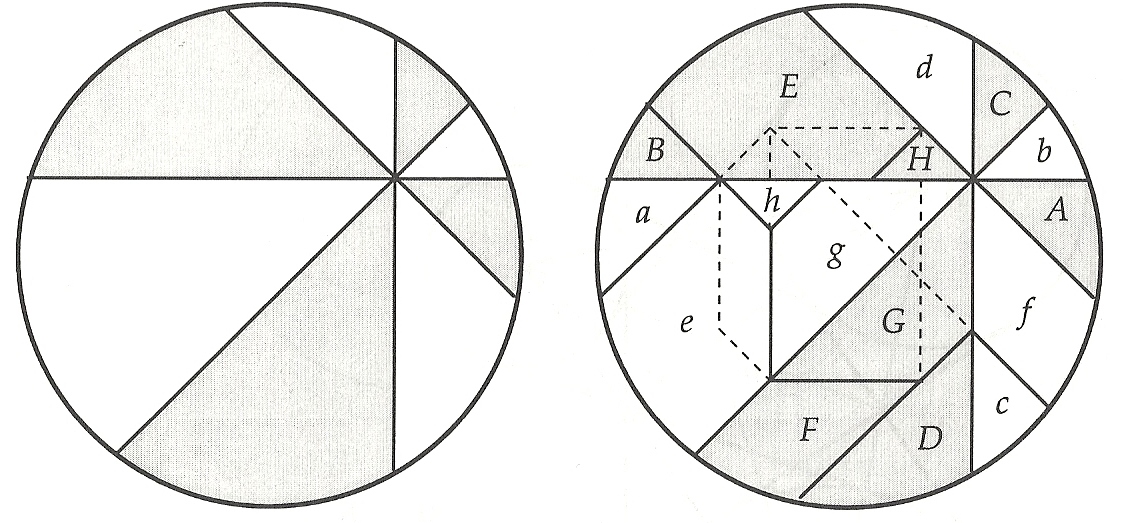
La idea del Teorema de la Pizza es hacerlo con cuatro cortes de la manera tradicional pero con el centro del corte en cualquier parte de la pizza. Por ejemplo, si hacemos unos cortes así:
Pero en verde y cafecito. Podemos enunciar esto de manera más o menos formal para obtener el siguiente Teorema. Claro que donde dice "pizza" podrías leer "círculo" para un teorema un poco más general.
La idea del Teorema de la Pizza es hacerlo con cuatro cortes de la manera tradicional pero con el centro del corte en cualquier parte de la pizza. Por ejemplo, si hacemos unos cortes así:
Entonces, lo que estamos diciendo es que el área blanca y el área gris son iguales. Por ejemplo:
El teorema no es complicado de demostrar y es algo visualmente muy interesante. Por ello nos vamos a centrar no solo en el Teorema, lo vamos a usar como excusa para mostrar distintas maneras de presentar y hablar de las matemáticas.Teorema de la pizza: Si una pizza es dividida en ocho trozos, obtenidos mediante cuatro cortes que pasan por un punto común y forman un ángulo de 45º entres ellos, entonces la suma de las áreas de los trozos alternos son iguales.
Donde, en la figura de la derecha, las áreas que tienen la misma letra son iguales, usando la minúscula para la región blanca y la mayúscula para la región sombreada. A lo mejor toma un rato convencerte y, para ser bien, bien formal quizás haga falta mostrar que los pedazos son de hecho iguales pero este es uno de esos momentos en que vale la pena no decir nada más.
Usar GeoGebra para mostrar esta clase de Teoremas es una herramienta invaluable en matemáticas para ayudar a convencer a la gente de que lo que acabamos de demostrar es de hecho cierto. Es decir, ya la imagen anterior demuestra el teorema, pero con el applet de aquí arribita es muy fácil convencerse de que es así de verdad.
Para (no) hacer en casa
Por supuesto que fuimos a comprar una pizza e intentar comprobar el teorema. Pide permiso a tus padres o algo así y, sobre todo, no vayas a desperdiciar una pizza perfectamente buena.
Sin embargo, siguiendo la idea de usar más de una manera de mostrar y demostrar teoremas matemáticos, ir por tu pizza y partirla no es tan mala idea. Debes tener en mente -como insistimos en el video- que una pizza real tiene volumen y densidad no-uniformes y que el Teorema de la Pizza está enunciado para áreas.
Para aprender más
En esta entrada del blog Cultura Científica hablan no solo lo que pasa con cuatro cortes, también con dos y tres cortes. Además, consideran el caso cuando tenemos orilla rellena de queso. La entrada está padrísima, tiene historia y un par de teoremas adicionales de pizza.
El grandísimo Adrián Paenza tiene una charla en TEDxRíodelaPlata y una de sus anécdotas empieza precisamente con una vez que quiso mostrar el Teorema de la Pizza. En realidad nunca habla del Teorema pero lo usa como excusa para hablar de otras cosas; la plática en sí vale mucho la pena.
El applet de GeoGebra lo diseñó Fabián Colombo en su página web, puedes visitar el original acá.
Básicamente repite lo mismo que escribimos aquí, pero puedes leer la entrada de Wikipedia sobre el Teorema della Pizza, en italiano. Ya sabes, para sentirlo más correcto.
La imagen de la pizza con Teorema de Pitágoras y la idea en sí la aprendimos de Walter Whiteley en MathCentral.





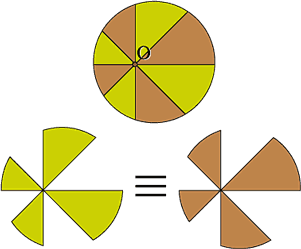
No hay comentarios.:
Publicar un comentario