Geometría redonda y aviones

Un oso camina

Un acertijo común -no sé qué tan matemático- es sobre un oso que camina. El acertijo dice más o menos así:

Un oso camina 10km al sur, luego 10km al este, luego 10km al norte, regresando al punto de partida. ¿De qué color es el oso?

En un primer momento, este acertijo podría parecerse a otros acertijos clásicos un-poquito-molestos (como el del tren eléctrico que viaja de norte a sur, o el del cerillo, la vela, la antorcha y la estufa) que parecen más adivinanzas y que con frecuencia se usan para mostrar que yo sé más que tú, lero lero. 

Sin embargo, este acertijo nos permite razonar más que sobre las palabras que te dijeron, sobre lo distinto que es la geometría en una esfera comparada a un plano. Es un buen ejercicio para tomar un globo terráqueo y tratar de encontrar la respuesta. 

Triángulo 90-60-90

Se podría intentar desestimar el problema de manera inmediata diciendo que es una tontería, que no se puede saber el color del oso con semejante información. Habrá quienes, en cambio, empiecen por hacer un mapa del recorrido. El mapa podría ser algo así: 

Si yo saliera de mi casa e intentara esta misma ruta -suponiendo que puedo atravesar las casas de mis vecinos- difícilmente regresaría al mismo punto; es más, probablemente terminaría a casi exactamente 10kilómetros al este de mi casa. 

Aquí ayuda mucho recordar que la Tierra -contrario a lo que piensan algunos- no es plana. Es más o menos una esfera y, para este acertijo, no hace mucha diferencia pensarla así. Luego, nuestro siguiente paso útil -en caso de que no tengamos un globo terráqueo o una pelota a la mano- sería dibujar un círculo y pensar dónde podríamos crear una ruta cerrada con las instrucciones que le dieron al oso.

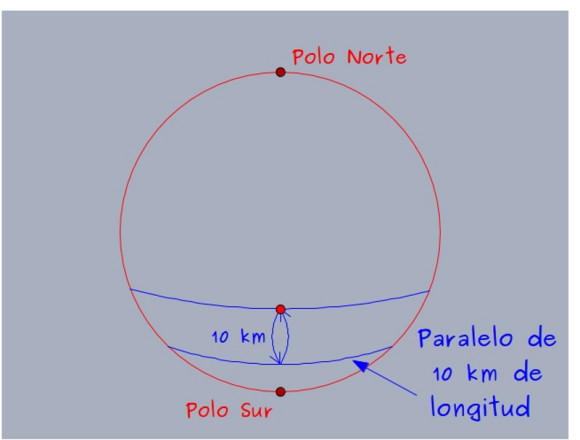
No cuesta mucho trabajo descubrir dónde es eso posible: el oso empezó en el polo norte, en un Ártico con más hielo que el actual. Por lo tanto, el oso es blanco. (Hay muchos otros lugares en la tierra donde esto es posible pero, creo, es el único que tiene osos.)

Parte del problema es construir una ruta cerrada (que empiece y termine en el mismo punto) con solo tres segmentos y dos giros de 90 grados. La única figura que podríamos formar es un triángulo, pero los ángulos interiores suman 180, ni más ni menos. ¿Cómo funciona?

Así que dos rutas que en un plano serían paralelas, si apuntan al norte entonces en realidad forman un triángulo cuyo tercer vértice es el polo. Es decir, aunque lo parezcan en el mapa, los meridianos no son paralelos (los paralelos sí lo son).  

El secreto es dejar de pensar en el plano y movernos a la esfera. Los triángulos que dibujemos sobre la superficie de una esfera son un poco peculiares: desde cierto punto de vista, sus lados son rectos; desde otro, son arcos de circunferencia. Sobre todo, sus ángulos no suman 180 grados y no tienen un valor fijo: la suma de los ángulos interiores puede ir desde 180 hasta 540 grados. 

¿La Tierra no es plana?

Existe un movimiento tomando fuerza que defiende la idea de que la Tierra es en realidad plana y su supuesta esferidad es una conspiración del gobierno para que muchas corporaciones se enriquezcan e ignoremos nuestro sentido común. 

Sí, en serio. 

Como toda buena teoría de conspiración, incluye un pacto entre todos los gobiernos del mundo para impedir navegar a la Antártida que, según ellos, es una enorme muro de hielo que impide que nos caigamos del planeta. El hecho de que la ONU use el mismo mapa que ellos es toda la evidencia que necesitamos. 

La teoría tiene otras explicaciones y argumentos bastante originales para darle consistencia y llenar huecos. Por ejemplo: Luna y Sol forman un sistema que rota sobre la Tierra plana, proyectando únicamente un cono de luz sobre una parte del planeta porque el Sol es mucho más pequeño de lo que nos dicen, que explica por qué no todos tenemos la misma luz al mismo tiempo. 

Admito que esto es increíblemente creativo. Es una de las cosas más brillantes que se me ocurren son más o menos consistentes si quisiéramos contestar por qué el mundo es como es suponiendo que el mundo es distinto. Con esto en mente, no podemos contestarles que la Tierra es esférica por geometría básica, que se sabe desde los griegos antiguos. Su Tierra es plana dentro de un universo que funciona completamente distinto al nuestro. 

Pero vale la pena recordarlo para nosotros. Cuenta la leyenda que Eratóstenes mandó un regimiento de soldados, dando pasos del mismo tamaño, para medir la distancia entre Alejandría (Egipto) y Siena (hoy Asuán, Egipto). Otros dicen que sencillamente usó la distancia que usaban los mercaderes de la época: 50,000 estadios. 

Durante el solsticio de verano, los rayos caen perpendiculares sobre Siena al medio día, pues está sobre el trópico de Cáncer. En Alejandría, observó que los rayos hacían una sombra a 7.12 grados, que es aproximadamente 1/50 de los 360 grados. Dado que podemos suponer que la Tierra y Sol están lo suficientemente retirados como para que los rayos de luz que pegan son todos paralelos, la conclusión natural es que la Tierra es esférica y podemos, con la inclinación, calcular su tamaño. Haciendo la sencilla regla de tres, la circunferencia de la Tierra sería aproximadamente 250,000 estadios. 

No solo su idea fue brillante; sus cálculos fueron increíblemente cercanos a la medida real. Por supuesto, los terraplanistas están de acuerdo en que el Sol no pega igual en todas las partes de la tierra, pero, como ya vimos, su conclusión es muy diferente: el Sol es más pequeño de lo que se cree y está mucho más cerca, de modo que actúa básicamente como una lámpara. Algo muy parecido pasará con su argumento sobre las rutas aéreas.

Los tierraplanistas han convencido a cientos o tal vez hasta miles de personas. Según ellos, es sencillamente "sentido común" el hecho de que sea plana, es la solución más sencilla a la que sin duda llegaríamos si no hubiésemos sido contaminados por la educación del gobierno. (Incluiría enlaces a los videos pero son demasiado convincentes y no quisiera llevarles por mal camino.)

Sobre esos aviones...

Uno de sus argumentos fuertes es la ruta que siguen los aviones.  De hecho, los aviones en sí son argumentos que usan con frecuencia: por ejemplo, la idea de que la misma ruta debería hacer menos tiempo a favor de la rotación de la tierra que en contra, o de cómo las fotos desde el avión no pueden capturar la curvatura. Las rutas tan extrañas que siguen los aviones son líneas rectas en su mapa plano: ergo, Tierra plana. 

Yareli detesta a los tierraplanistas pero en su reciente viaje cruzando el Atlántico estaba demasiado dormida para revisar el monitor. Si lo hubiera hecho, habría podido revisar que, efectivamente, un viaje México-Europa no cruza el mar en línea recta sino que viaja hacia el norte, como si fuera a Nueva York, una ruta que es casi línea recta en el mapa terraplanista con los puntos marcados con DAL-NYC-PARIS. ¿Por qué siguen esta ruta tan extraña?

No parecen darse cuenta que han llegado a una conclusión brillante y una manera muy didáctica de demostrar cómo se ven las geodésicas en la Tierra, pero con hipótesis muy diferentes. Para ello, tenemos que empezar a hablar de nuestros mapas y sus respectivas proyecciones. 

Dado que la Tierra es esférica, es sumamente complicado representarla adecuadamente en un plano, es decir, un mapa. Los mapas que tenemos son proyecciones y cada uno de ellos tiene ciertos problemas y deformaciones. El mapa más famoso que tenemos, la proyección de Mercator exagera terriblemente el tamaño de los países más al norte como Groenlandia, Rusia o Canadá; aunque parecen casi del mismo tamaño, África es 14 veces más grande que Groenlandia y Brasil es 5 veces más grande que Alaska. Esto es sumamente controversial para la geopolítica mundial (ver: proyección de Gall-Peters) pero las proyecciones cilíndricas -como la de Mercator- son sumamente prácticas para la navegación pues norte-sur se ve arriba-abajo y este-oeste se ve derecha-izquierda. 

Pero a lo mejor no es la más exacta. ¿Cuál te gusta más a ti? Tenemos proyección de Goode, de Albers, de Vansant, de Waterman. 

Todas las proyecciones tienen su parte matemática, por supuesto. El procedimiento no es muy distinto al que se hace intuitivamente en diseño con perspectiva y proyecciones. No por nada usamos la palabra mapeo cuando hablamos de ciertas funciones. Algunas de estas proyecciones preservan ciertas propiedades: distancias (métricas), tamaños, direcciones. 

La proyección que usan los tierraplanistas en su mapa, es decir, la proyección usada para el mapa que aparece en la bandera de las Naciones Undias es una proyección acimutal o cenital, donde se proyecta la esfera sobre una superficie tangente a ésta. Tiene simetría radial y los grandes círculos (los meridianos) se ven como líneas rectas, mientras que los paralelos se ven como círculos concéntricos. El resultado es parecido (aunque no idéntico) al que se usa con una proyección cilíndrica. 

Estamos listos para encontrar la razón detrás de la coincidencia tierraplanista: la proyección cenital, dijimos, hace que algunos grandes círculos se vean como líneas rectas. Estamos muy acostumbrados a pensar la distancia más corta como una línea recta, porque esto siempre ocurre en el plano. En la esfera no es así: la geodésica, o distancia más corta, es en realidad el arco del gran círculo que pasa por esos dos puntos. (Usando alguna de estas páginas web podrías ver cuál es el gran círculo que pasa por dos ciudades que tú quieras y comparar cómo se ve contra la línea recta en el mapa.)

¿Por dónde se van los aviones? Bueno, no son enchiladas. Sería natural pensar que el avión tomaría la ruta más corta (el arco del gran círculo) pero intervienen también tratados internacionales y leyes de aviación (recuerda que el espacio aéreo es también territorio nacional). ETOPS, por ejemplo, dice cuál es la máxima distancia a la que un avión puede estar de un aeropuerto en cualquier momento del vuelo, por aquello de las emergencias.

Así que, si alguna vez tienes oportunidad de viajar lejos y observas una ruta extraña en el monitor del avión, no vayas a pensar en conspiraciones gubernamentales; piensa en matemáticas.