La tortuga maratonista
Hace muchísimos años, un griego llamado Zenón concibió una serie de paradojas para tratar de mostrar que el movimiento es imposible -y, que si lo aceptamos, sin duda llegaríamos a absurdos. Una de ellas, quizás la más famosa, trata de Aquiles -el gran guerrero de la época- y una tortuga -el paradigmático corredor lento pero seguro-.Aquiles, el atleta más veloz, capaz de correr los 100 m. en 10 segundos, no podrá alcanzar a una lenta tortuga, diez veces menos rápida que él. Ambos disputan una carrera, concediendo Aquiles una ventaja de 100 m. a la tortuga. Cuando Aquiles ha cubierto esos 100 m., la tortuga se ha desplazado 10 m. Al cubrir Aquiles esos 10 m., la tortuga se ha desplazado 1 m. Mientras cubre ese metro que le separa de la tortuga, ésta ha recorrido 0'1 m. Y así indefinidamente.Así, Aquiles debe cubrir infinitos trayectos para alcanzar a la tortuga. Por lo tanto, Aquiles deberá cubrir una distancia infinita, para lo cual necesitará un tiempo infinito. De tal manera que el desgraciado Aquiles nunca alcanzará a la tortuga.
Como ves, la moraleja de esta paradoja y la fábula de la liebre y la tortuga (no sabemos si es la misma tortuga, pero no lo descartamos); mientras que la carrera que pierde la liebre es una importante lección en no confiarse y en perseverar, la carrera de Aquiles puede dejarte creyendo que todo esfuerzo es inútil y es mejor no intentarlo.
Sin embargo, hay algo en la carrera de Aquiles que suena muy problemático. La cosa es que hemos visto carreras donde alguien que va detrás termina ganando. Es más, Zenón implica que el movimiento es imposible porque, para llegar a cualquier lugar tendrías que primero recorrer la mitad del camino, luego la mitad de la mitad, luego la mitad de la mitad de la mitad, de modo que siempre falta un pedazo. Sin embargo, el movimiento es posible.
Por el otro lado, hay escenarios entre Aquiles y la tortuga -con algunas condiciones ligeramente cambiadas- donde, efectivamente, Aquiles jamás la alcanzaría. Todo cortesía de nuestro viejo amigo Infinito.
Sumar infinitos números
La paradoja de Aquiles y la tortuga nos va a servir como analogia para explicar algunas series especiales. A diferencia de la televisión, en matemáticas una serie es, sencillamente, una suma infinita. Por supuesto, esto puede parecer complicado en un primer momento pues, si sumas infinitos términos, nunca terminarías.
Una manera común de lidiar con esto en matemáticas es hablar de límite, que es un concepto al que intentaremos aproximarnos lo más que podamos esta vez. La cosa es que, sin hacer infinitas sumas, a veces podemos tener una idea muy clara de cuál debería ser el resultado de dicha suma.
Antes de empezar, vamos a definir "ventaja" en nuestro problema de Aquiles y la tortuga. En el planteamiento original de Zenón, Aquiles le dio cierta ventaja inicial a la tortuga; después, vamos a entender por ventaja la distancia que debe recorrer Aquiles cuando llegó al punto donde estaba la tortuga antes. En el planteamiento original de Zenón, la ventaja inicial podría ser 1km, después 100m, 10m, 1m, etcétera.
Podemos empezar, siguiendo con Aquiles y la tortuga, proponiendo algunas condiciones necesarias sencillas de ver. Por ejemplo, si la tortuga corriera más rápido que Aquiles, es decir, si cada vez que Aquiles llega al punto donde estaba la tortuga la ventaja se hizo más grande, entonces claro que nunca la alcanzará. De hecho, si corren a la misma velocidad, entonces la ventaja nunca se acorta y Aquiles correría detrás de la tortuga toda la eternidad, un problema que asustaba a toda mi generación
Hemos encontrado una condición necesaria: Aquiles tiene que correr más rápido que la tortuga. Es decir, si la quiere alcanzar, es absolutamente necesario que la ventaja se vaya reduciendo más y más hasta que pueda ser prácticamente 0.
Tristemente, aunque parezca difícil de creer, esta no es una condición suficiente. Es decir, Aquiles podría ir acortando la distancia, que la distancia cada vez sea más pequeña y más pequeña y, sin embargo, no la alcanza. Parece contradictorio afirmar que la distancia se hace 0 y, sin embargo, no la alcanza. La cuestión es que, para que la ventaja se haga 0, Aquiles tendría que recorrer primero una cantidad infinita de kilómetros. Es decir, no es nada más el tamaño de la ventaja sino, también, la suma de las ventajas.
Helio, Neón, Argón, Zenón y Radón
Vamos a ponernos un poco más matemáticos aquí.
Con las "ventajas" como las hemos definido estamos construyendo una sucesión. Por ejemplo, la que proponía Zenón es la siguiente sucesión:
1000m, 100m, 10m, 1m, 0.1m, 0.01m, 0.001m,...
Esta sucesión es infinita, como lo indican los puntos suspensivos. También existen sucesiones finitas pero esas no son tan interesantes aquí. Además, el ejemplo cumple la condición que hemos pedido: cada término en la sucesión se hace 10 veces más pequeño, de modo que se va haciendo cada vez más parecido a 0.
Luego, estamos interesados en la suma de las ventajas. En nuestro ejemplo, Aquiles recorrería:
1000m + 100m + 10m + 1m + 0.1m + 0.01m + 0.001m + ...
Esta suma puede ser igualmente infinita -en la cantidad de términos que suma- si los tomamos de una sucesión infinita. A esta suma le llamamos serie. En el lenguaje común, serie y sucesión a veces se usan de manera intercambiable; en matemáticas tienen significados claramente distintos.
A cada término de la sucesión y a cada suma parcial podemos asignarle un número natural. Es decir, el primer término, el segundo, el décimo, etcétera. La suma de los primeros 4 términos es:
1000 + 100 + 10 + 1 = 1111.
La condición de que cada término se haga más y más pequeño es pedir que la sucesión converja a 0 (estamos conjugando el verbo converger). Esto es, que el n-ésimo término se aproxime a 0 conforme n se aproxima a infinito.
Estamos pidiendo que converja a 0, pero las sucesiones pueden converger a cualquier cosa. Esa "cosa" se llama límite. Por ejemplo, la sucesión 1, 1, 1, 1,... converge a 1.
Hay distintas maneras en que una sucesión o una serie pueden no converger. Por ejemplo, la sucesión 1, 2, 3, 4,... se está yendo a infinito, porque cada vez más grande; en este caso, según el contexto, se puede decir que la serie diverge -es decir, que no converge- y, también, que converge a infinito. (Es una manera extraña de no tener límite: que el límite sea infinito.)
Dicha distinción se hace porque hay maneras más feas de no converger. Por ejemplo: la sucesión 1, -1, 1, -1, 1, -1,... no tiende a absolutamente nada, pues un momento está en 1, al siguiente en -1, y nunca se detiene.
Demostrar la convergencia de series no es una cosa sencilla. De hecho, Euler saltó a la fama matemática internacional a los 28 años luego de resolver el problema de Basilea, una pregunta abierta de casi 90 años sobre la convergencia de la serie de los recíprocos de los cuadrados.
Para la convergencia de una serie pedimos que la sucesión de sus sumas parciales (en el ejemplo serían 1000, 1100, 1110, 1111, 1111.1, 1111.11,...) tenga un límite. Hay varias maneras de mostrar la convergencia o no de algunas series. Uno
La estrategia de Aquiles
No es fácil salir del atoradero en que nos metió Zenón. Algo tiene que estar mal, pero el razonamiento parece bueno. Parte del truco es la manera en que Zenón nos obliga a pensar el mundo físico. Afortunadamente, la serie que escogió Zenón converge, de modo que podemos zafarnos de su trampa.
La versión que escribimos de la paradoja dice que Aquiles corre 10 veces más rápido. Otra paradoja del movimiento de Zenón dice que una piedra no puede llegar a su destino pues siempre debe recorrer la mitad del camino que le falta, de modo que siempre le falta una mitad, por pequeña que sea. Si nos fijamos en este ejemplo (o bien, "Zenón corre dos veces más rápido que la tortuga") podemos ver lo que sucede:
Zenón no mentía: efectivamente, Aquiles tendría que hacer una suma infinita. Lo que ocurre es que esa suma infinita no es, de hecho, infinito; es 1. Si Aquiles le dio 1km de ventaja a la tortuga y corre dos veces más rápido que ella, claramente la alcanza después de 2km y el mundo tiene sentido de nuevo.
Si necesitas otra imagen para convencerte, acá va:
Vamos a intentar hacer más que demostrar las cosas con imágenes. Pero las imágenes son muy bonitas en este caso. ¿Qué pasaría si Aquiles corre 4 veces más rápido que la tortuga, y le da 1km de ventaja? Cuando Aquiles corre 1km, la ventaja ahora es de 250m; cuando Aquiles corre 250m, la ventaja es ahora 62.5 km...
Vamos a intentar hacer más que demostrar las cosas con imágenes. Pero las imágenes son muy bonitas en este caso. ¿Qué pasaría si Aquiles corre 4 veces más rápido que la tortuga, y le da 1km de ventaja? Cuando Aquiles corre 1km, la ventaja ahora es de 250m; cuando Aquiles corre 250m, la ventaja es ahora 62.5 km...
En la imagen, cuando Aquiles alcanza a "correr" el triángulo completo, la tortuga únicamente "corre" la tercera parte. Aquiles la alcanza justo en 1.333... km, pues cuando la tortuga corre 1/3, Aquiles pudo correr 4/3.
¿Y si la ventaja hubiera sido de 2km? No mucho cambia. Aquiles la sigue alcanzando después de 4/3 veces 2km, es decir, en la marca de 2.666... km.
Si ambos corren a una distancia constante -y, como habíamos señalado, Aquiles corre más rápido-, entonces estamos trabajando con una serie geométrica. En una sucesión geométrica, cada término de la sucesión se obtiene del anterior multiplicando siempre por el mismo factor. Por ejemplo 3, 6, 12, 24, 48,... es una sucesión geométrica con factor 2; y 1, 1/2, 1/4, 1/8,... es una sucesión geométrica con factor 1/2.
Si el factor es mayor a 1, entonces quien corre más rápido es la tortuga, pues las "ventajas" (es decir, los términos en la sucesión) se están haciendo más grandes. En ese caso, la serie se va a infinito y Aquiles nunca la alcanza. Si el factor es exactamente 1, la sucesión es constante (la ventaja nunca se acorta) y Aquiles tampoco la alcanza jamás.
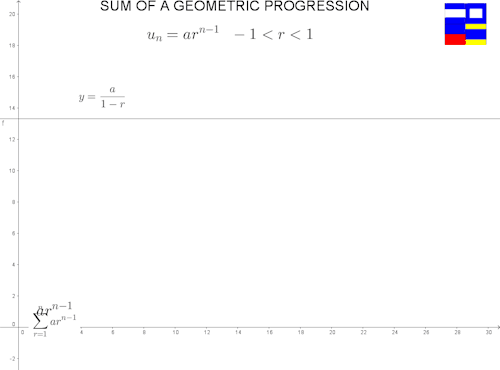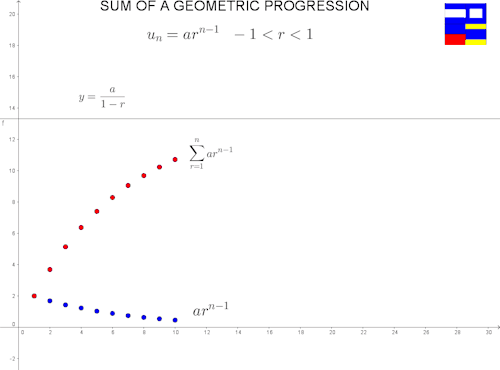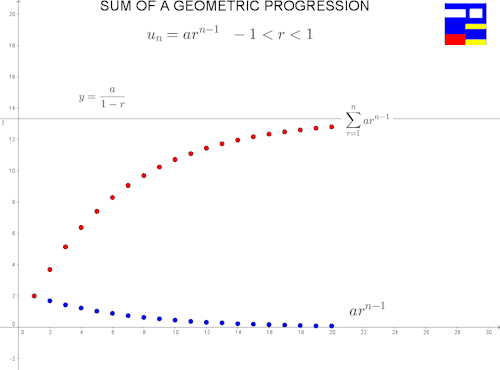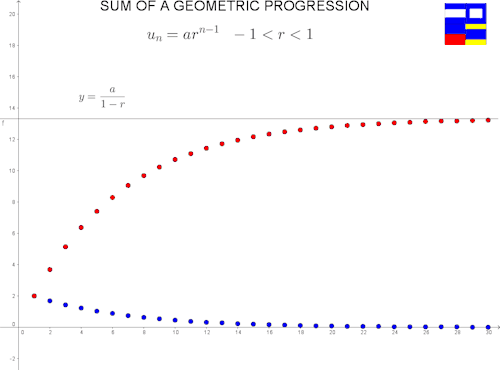
¿Qué pasa si el factor es positivo, pero menor a 1? Aventamos la imagen primero:
En todos esos casos, la serie tiene un límite. Es decir, converge. La prueba no es muy complicada y, salvo la parte del límite, únicamente usa una fórmula conocida.
Si Sn es la suma de los primeros n términos de tu sucesión, entonces hacemos un viejo truco:
y encontramos una expresión alternativa y mucho más útil para Sn. Esta sería una suma parcial. En esta notación, r representa el factor de nuestra sucesión geométrica. Si n se hace más grande, r^n se hace más pequeño. De hecho, se hace 0, que es algo que habíamos pedido.
Por ejemplo, para la sucesión 1, 1/2, 1/4, 1/8, 1/16,... a = 1, r = 1/2. Lo que nos queda es
1/(1 - 1/2) = 1/(1/2) = 2.
Que es lo que la imagen y nuestra intuición nos habían dicho. Si lo hacemos para 1, 1/4, 1/16, 1/64,... tenemos que a = 1, r = 1/4. Nos queda:
1/(1 - 1/4) = 1/(3/4) = 4/3.
Basta con que Aquiles corra más rápido que la tortuga y que ambos corran a velocidad constante para que la sucesión de sus ventajas se exprese como una sucesión geométrica. En todos esos casos, Aquiles empata... y caballo que alcanza no se le mira el diente.
Denle chance a la tortuga
No vamos a permitir que la tortuga gane únicamente por fines moralistas y le vamos a dar también ventaja matemática. Conociendo algunas series divergentes, es posible construir escenarios en que Aquiles corre más rápido y, sin embargo, la tortuga gana.
Por ejemplo, como sabemos que la serie armónica
1 + 1/2 + 1/3 + 1/4 + 1/5 + ...
diverge, nos aventamos a construir el caso. Y aquí parece que rompemos una condición: Aquiles sí corre más rápido, pero se va cansando. Es decir, su velocidad no es constante. Sin embargo, es verdad que (1) corre más rápido, y que (2) la ventaja se va haciendo más y más pequeña, hasta llegar a 0.
Usando cualquier serie divergente podemos construir un ejemplo similar. Por ejemplo, la de los inversos de los números primos, que demostró Euler.
 |
| Serie Divergente |
Olimpiada de Otoño
Hemos experimentado con series geométricas en la pasada Olimpiada de Otoño. Uno de los ejercicios es más sencillo que los otros dos y es justo el que vamos a explicar. Los otros dos se dejan como ejercicio al lector (pero están bonitos, en serio).
Problema 1. (II Olimpiada Femenil de Matemáticas, U13) Dany y Misshy corren en una pista circular de 1km. Salen al mismo tiempo pero Dany corre cuatro veces más rápido que Misshy. Coinciden de nuevo cuando Dany ha dado cuatro vueltas y Misshy la primera; ¿cuántas veces antes coinciden? ¿En qué puntos de la pista coinciden?
Este es un problema parecido al de Aquiles y la tortuga. La diferencia es que no hay ventaja y que corren sobre una pista circular (bastaría con ser cerrada).
Como Dany corre 4 veces más rápido, cuando Dany lleva 1 vuelta, Misshy lleva 1/4. Cuando Dany lleva 1 + 1/4 de vuelta, Misshy ha recorrido 1/16. Cuando Dany lleva 1 + 1/4 + 1/16 de vuelta, Misshy ha recorrido 1/64 adicionales. Como ya vimos en una imagen más arriba, Se deben alcanzar en 1/3 de la pista, es decir, justo en la marca de 0.333 kilómetros.
Sin embargo, esto es entender el problema à la Zenón. Podemos pensarlo de otra manera: como Dany corre 4 veces más rápido, va a dar 4 vueltas cuando Misshy complete la primera. Esa debe ser la 4 vez que se encuentren -pues se encuentran una vez por cada vuelta de Misshy- y la primera ocurre justo en la salida. Las otras dos -intermedias- deben complir que entre vez y vez que se encuentran, Misshy recorra la misma porción de pista. Como se encuentran en 0 y en 1, tienen que encontrarse en 1/3 y en 2/3.
Acabamos, sin querer, de demostrar que 1 + 1/4 + 1/16 + 1/64 + ... = 1/3. Y este mismo argumento funciona para cualquier n veces más rápido, que es el siguiente ejercicio.
Problema 2. (VI Olimpiada de Otoño, W13) Totoro, Nala y Canela corren en una pista circular de 1km. Totoro corre dos veces más rápido que Nala y tres veces más rápido que Canela. Se vuelven a encontrar en la salida cuando Totoro ha dado 6 vueltas. ¿En qué otros puntos de la pista se encuentra Totoro con alguna de ellas? ¿Con quién?
Los dos siguientes también involucran series geométricas, pero de maneras más interesantes y creativas.
Problema 3. (VI Olimpiada de Otoño, C20) Un número es cachorro si sus únicos factores primos son 2, 3 y 7. Por ejemplo: 8, 42, 2016. La suma de los recíprocos de los cachorros no-cuadrados se puede expresar como a/b en su expresión simplificada. Calcula ab.
Problema 4. (VI Olimpiada de Otoño, U20) El producto de los lados de un triángulo es 2040. El área del triángulo es 60. El circunradio de este triángulo es R0. Se construye un triángulo equilátero de lado R0; llamamos R1 a su circunradio. Se construye un nuevo triángulo equilátero de lado R1 y el proceso se repite infinitamente. Encuentra la suma R0 + R1 + R2 + ...
Por supuesto, esto quiere decir que nos tenemos que inventar problemas nuevos.
Para saber más
Tomamos la versión de la paradoja de Aquiles y la tortuga de este enlace en catedu.es, autoría de José María Sonado Muzás, donde también toca el tema de las series y sumas infinitas.
Este artículo en Slate.com, de Brian Palmer, contiene el ejemplo donde Aquiles efectivamente no alcanza a la tortuga. Además, contiene de manera muy concisa una defensa contra la paradoja que parece ridícula pero puede tomarte por sorpresa.
El viejo "problema" de 1 + 2 + 3 + ... = -1/12 también fue parte de la motivación pero es un asunto demasiado complejo para tratar en esta entrada tan breve. El artículo es de Hammond, publicado en Science de The New York Times.
Es sabido que soy fan de Euler. En las referencias de Wikipedia al artículo del problema de Basilea puedes encontrar tres artículos muy interesantes sobre la historia y solución del problema.








Dios! ahora mi vida no tiene ningun sentido...¿y si eliminamos el infinito de nuestras vidas? digo xD
ResponderBorrar