Hay ciertos números que son muy importantes en las matemáticas: 0 y 1, por ejemplo, son dos enteros bastante populares por sus propiedades de no afectar la suma o el producto, pero también tienen una relación interesante en los exponentes. podríamos además hablar de e, el número de Euler -porque lo bautizó, no porque lo descubrió, porque así de importante era Euler-, la base del logaritmo natural, aproximadamente 2.71828, aparece en el interés compuesto, límite de funciones y sumas muy bonitas; podríamos también hablar de phi, la razón áurea, proporción divina, más o menos 1.6180339, el número ese con el que construyes caracoles y antiguos templos griegos. Sin embargo, el honor quizás se lo lleve pi, π, que aparece en casi cualquier lugar.
¿Cuántos números tienen el honor de aparecer en el calendario? Bueno, sí, los naturales del 01 al 12 y del 01 al 31, pero π es el único al que le hacemos fiesta cada 14 de marzo (3-14 en la nomenclatura norteamericana).
Cierto, los decimales de e y phi hacen que eso sea un poco más complicado, pero no es tema aquí. Algunos aparecen en la identidad de Euler, la llamada ecuación matemática más hermosa de la historia del mundo mundial, consecuencia de la fórmula de Euler:
¿Por qué aparece π en el círculo y no otro número?
La primera cosa de la que debemos convencernos es que en cualquier circunferencia, sin importar el tamaño, la razón del perímetro y el radio es constante. Primero, vamos a convencernos que es así en los polígonos regulares. Todos los triángulos equiláteros son semejantes entre sí, si dividimos su perímetro entre el lado, el valor es constante y siempre igual a 3; todos los cuadrados son semejantes entre sí, si dividimos su perímetro entre el lado, el valor es constante y siempre es igual a 4; en los pentágonos regulares, la razón sería siempre 5 y así sucesivamente. Ahora, tendríamos que ver que todos los círculos son semejantes entre sí y de ahí, pensar que lo mismo debe ser cierto: el valor de su perímetro entre su radio debe ser constante. (En un polígono regular, sabiendo el lado podemos trazar el polígono; en un círculo, sabiendo el radio podemos trazar el círculo.)
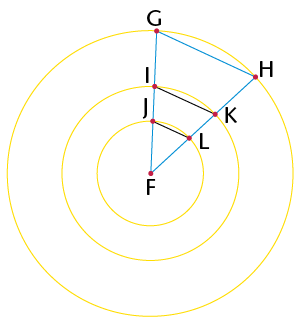
Podemos intentar una demostración más formal: aproximando al círculo con polígonos regulares inscritos a él de cada vez más lados. Lo hacemos para dos círculos concéntricos. Luego, trazando los triángulos isósceles que tienen al centro como uno de los vértices y al lado del polígono como uno de sus lados, es fácil convencernos de que estos dos triángulos son semejantes. Luego, la razón entre el lado y el radio es la misma en ambos triángulos. Como el perímetro del círculo sería el límite de la suma de los lados cuando la cantidad de lados crece y crece, la razón entre el perímetro y el radio debe ser la misma para ambos círculos.
Así, nos convencemos de que la razón entre la circunferencia y su radio es constante. Como el diámetro es siempre el doble del radio, la razón entre la circunferencia y el diámetro también es constante y ese valor constante es π. Es decir, esa es precisamente nuestra definición del número π: es la razón entre la circunferencia y el diámetro de un círculo cualquiera. (Nota: no hemos dicho cuánto vale, simplemente lo hemos bautizado.) Por cierto que para algunos matemáticos sería mejor olvidarnos de π y pensar en tau, que es 2π y que es, ahora sí, la razón entre la circunferencia y el radio.
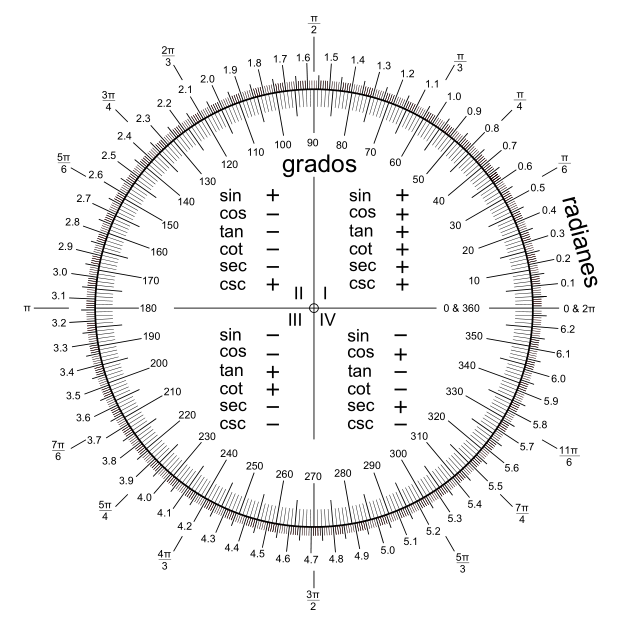
Antes de empezar a averiguar cuánto vale, saber que esa razón es constante tiene una consecuencia bastante útil: podemos dividir la circunferencia en 2π pedacitos iguales, cuyo tamaño varía entre círculo y círculo en función del radio. Además, podemos hacer asociaciones entre la cantidad de pedacitos y los ángulos desde el centro del círculo; por ejemplo, si marcamos un ángulo de 90º siempre tenemos un cuarto de circunferencia, por lo que tenemos exactamente π pedacitos. Esos "pedacitos" se llaman radianes y son otra forma de medir ángulos en circunferencias en función precisamente del radio -y de ahí su nombre. Entonces, los ángulos en un círculo podemos decir que van desde 0 hasta 2π.
(Estos radianes van a ser importantísimos para las demostraciones que usan el Cálculo, que vamos a tratar de sacarles la vuelta.)
¿Cuánto vale π?
Ya definimos π pero todavía no sabemos cuánto vale. Hay una gran historia de las aproximaciones de π. Todos nosotros experimentamos cierta madurez: conforme crecemos, π pasa de valer 3.14 a valer 3.1416 a valer 3.14159, e incluso si esos tres números son distintos entre sí, nadie parece preocuparse demasiado.
Una de las respuestas más comunes cuando preguntamos "¿Cuánto vale π?" es "Infinito". Es cierto que π tiene una expansión decimal infinita, pero es un número más bien pequeño. Es tan pequeño, que si tuvieras 4 manzanas, definitivamente tienes más de π manzanas. Algunos datos curiosos: el matemático William Jones fue el primero en usar la letra griega π para referirse al número que ahora conocemos como π, en 1706; fue Leonhard Euler, para variar, el que popularizó su uso.
(Por cierto, todos los números tienen una expansión decimal infinita; vamos a demostrar que 1 = 0.999... y con esa idea debe quedar claro que si tu número tiene una expansión decimal finita, entonces también tiene una infinita:
También puedes hacerlo sumando tres tercios que definitivamente son un entero, pero también se expresan de manera infinita para llegar a la misma expresión. Así, por ejemplo, 12.093 = 12.092999... son dos nombres para la misma cosa.)
La primera aproximación -cronológicamente hablando- estaría en la Biblia: en 1 Reyes 7:23 dice que "Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos," de donde queda claro que para los antiguos hebreos, el perímetro era 3 veces el diámetro.
Hay otras aproximaciones conocidas de la antigüedad: para los Babilonios, π era exactamente 3.125, es decir 3 y un octavo, que no es tan mala aproximación; para los Egipcios, en el papiro de Rhind encontramos -además de las instrucciones para obtener el conocimiento de todas las cosas oscuras- la aproximación 3.16045 o 256/81, que se obtiene aproximando con polígonos. Brahmagupta dijo que π vale 3.1622 o raiz de 10, Ptolomeo dijo que π vale 3.14166, Arybhata dijo 3.1416 o 62832/20000, Liu Hui dijo 3.14159 y Zu Chongzhi llegó al impresionante valor de 3.141592920 o 355/113. Aquí hay una lista de aproximaciones famosas pre- y post- calculadoras.
La más famosa de todos es la de Arquímedes, quien usó un método que es una proeza de cálculo para su época, como una aproximación al perímetro con polígonos regulares inscritos.
Hay muchas otras maneras de encontrar el valor de π en matemáticas: es el límite de algunas series bastante interesantes y, todavía más, es el límite de algunas probabilidades muy curiosas (más de esto adelante). Por ejemplo, el producto de Wallis. Otro ejemplo, de Liebniz y otras fracciones continuas:
¿Por qué el área del círculo es π veces el radio al cuadrado?
Vamos a mostrar aquí algunas maneras de demostrar que la fórmula que conocemos para el área de un cuadrado. Las más intuitivas serán poco formales -requieren algo de imaginación y fe en el infinito-, las más formales serán quizás muy oscuras sin la ayuda del Cálculo.
Método 1: Rebanando la pizza.
Probablemente el método no se llama así, por cierto. La idea es rebanar el círculo en pedazos que tienen el mismo arco y acomodarlos para que asemeje un paralelogramo
Mientras más pedazos hagamos, menores serán los arcos y tendrá mucha mayor apariencia de paralelogramo
El lado grande del paralelogramo mide la mitad del perímetro, es decir π veces el radio, y la altura es exactamente el radio. Luego, el área sería π veces el radio al cuadrado.
Método 2: Rebanando la cebolla.
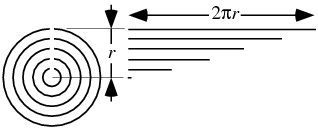
Imagina que tu círculo de radio r está hecho por infinitos círculos concéntricos, de radio menor o igual a r. La idea es cortar estos círculos interiores y "desenrrollarlos".
Podríamos volver a acomodarlos en orden, dejando uno de sus extremos alineado. Lo que nos queda es un triángulo rectángulo cuya base mide 2πr, porque es el círculo más grande desenrrollado, y la altura mide r, porque es lo que alcanzan a apilar tus círculos. Luego, el área de ese triángulo es π veces el radio al cuadrado.
Método 3: Formalizando la cebolla.
Lo que hicimos "desenrrollando" las capas de la cebolla no parece muy truculento, lo que parece sumamente mañoso es volver a apilarlos. La cosa es que estamos tomando franjas de círculo, cada uno tiene ancho 0 -porque son rectas- pero resulta que apilando infinitas de ellas obtenemos no solo un ancho distinto de 0, obtenemos un ancho fijo aunque los reacomoremos.
Lo que estamos haciendo es sumar sobre pedazos infinitesimales. Eso se hace integrando. Estamos sumando circunferencias -es decir, pedazos que miden 2πx- desde que x vale 0 hasta que vale r, el radio del círculo al que le estamos calculando el área. Esa integral se escribe así:
y se resuelve de manera muy sencilla.
Método 4: Inscribiendo polígonos.
La idea aquí es que mientras más lados tenga tu polígono, más se parece al círculo. Luego, si podemos hacer que el número de lados crezca y crezca, debemos obtener exactamente el área del círculo. Dicho polígono, por cierto, se llama apeirógono.
Si sabemos el área de uno de los triangulitos pequeños que van al centro, el área de todo el polígono es n veces uno de esos triangulitos. Es decir, la misma manera en que calculamos el área de un polígono regular común y corriente. Si recuerdas, el área de un polígono regular es perímetro por apotema sobre dos; mientras nuestro polígono se acerque al círculo, el perímetro se aproxima al perímetro del círculo, es decir, 2πr, y el apotema se aproxima al radio, es decir, el área sería π por radio al cuadrado.
Para verlo un poco más formal vamos a hacer poquita trampa y calcular el área de dicho triángulo usando trigonometría: como conocemos dos lados y el ángulo entre ellas, podemos calcular el área de cada triangulito usando la siguiente fórmula:
en nuestro caso particular, tanto a como b son radios, y el ángulo C es la n-ésima parte de mis 2π radianes. El problema aquí va a ser que nos creas el siguiente límite:
y obtenemos ya la fórmula del área. (En el límite, lo hicimos para un círculo de radio 1; si tu radio fuera r, como no depende de n, entonces no se afecta nada, nadita.)
Método 5: integrando con la definición del círculo
Cuando usamos un compás, lo que hacemos es dejar un punto fijo -que es el centro del círculo, el lugar donde se clava el lado que tiene punta- y luego marcar todos los puntos que están a una cierta distancia dada -por eso los mejores son los que no se abren a medio círculo-. En resumen, el círculo es el lugar geométrico de los puntos que están a una distancia dada -llamada radio- de un punto fijo -llamado centro-.
En Geometría Analítica pronto aprendemos que el Teorema de Pitágoras nos sirve para calcular distancias en el plano, así que podemos definir el círculo como todos los puntos que cumplen la siguiente fórmula:
donde (h, k) son las coordenadas del centro. Si tenemos nuestro círculo centrado en el origen y hablamos del disco, es decir, del círculo relleno y no solo de la circunferencia, nuestra fórmula queda así:
También, aprendemos -como aplicación sencilla de "la regla de la línea horizontal"- que un círculo no es una función, y al principio aprendemos a integrar nada más funciones. Eso se resuelve sencillo si tomamos únicamente la mitad de arriba del círculo. La función queda así:
que es, pues, medio círculo, más o menos:
Que es el primer tipo de integrales que aprendemos a resolver por sustitución trigonométrica. Los valores de x posibles van desde -r hasta r, que son los únicos puntos diametralmente opuestos en nuestro medio círculo. Sin entrar en los detalles de cómo resolver la integral, veamos que ésta arroja la fórmula deseada (recuerda que tenemos solo medio círculo):
Método 6: integrando en coordenadas polares
En el círculo unitario -el círculo de radio 1- usando las definiciones básicas de seno y coseno podemos ver que los puntos (x, y) sobre el círculo pueden ser vistos en función del ángulo a, como (cos a, sin a), pues la hipotenusa de los pequeños triángulos rectángulos que se forman es siempre 1. Si hacemos lo mismo con un círculo de radio R, las cosas no cambian mucho.
Eso nos da la idea de cambiar los ejes y, en lugar de marcar x, y marcamos theta y r, que son la distancia al origen y el ángulo sobre el eje x original. Estas nuevas coordenadas se llaman polares. En ese nuevo sistema de coordenadas, nuestro círculo original se ve como un rectangulito con uno de sus lados igual a 2π -que son los valores posibles del ángulo- y el otro igual a r, que son los valores que toma la distancia.
Desafortunadamente, esta transformación no preserva área, así que calcular el área no es nada más base por altura. Para calcular el área tenemos que hacer una integral muy bonita, que es una de las primeras que aprendemos a hacer cuando hacemos integrales de área o superficie:
(Para ver por qué integramos r, hay que recordar lo del jacobiano y lo de la sustitución para varias variables. Hay otra demostración de la fórmula que usa el Teorema de Green con la que sencillamente ya no nos vamos a meter aquí pero que puedes checar por tu cuenta.)
Para hacer en casa:
¡Calcula π aventando cosas al piso! Bueno, no cualquier cosa. Se trata de la Aguja de Buffon, una manera de calcular el valor de π como una probabilidad. Necesitas un palo, popote o palillo. Traza en una hoja líneas paralelas distanciadas tanto como la longitud del instrumento de tu elección -funciona bien con algunos pisos de mosaicos y los palitos de bandera de papelerías. Lanza el palo sobre la cuadrícula (hazlo girando o algo que sientas más o menos aleatorio). Cuenta el número de intentos y el número de veces que al lanzar el palito, éste cruza una línea. Entonces, puedes aproximar π como
el caso general con una varita de longitud L y rectas a distancia D es
Puedes revisar la demostración de por qué esto funciona -y la generalización- en esta liga.
Segundo: un acertijo. Imagina que tienes un listón que envuelve una pelota de fútbol por su "Ecuador". ¿Qué tan más largo tendría que ser tu listón para "flotar" a 2cm de la pelota? Ahora, un listón mucho más largo envuelve a la Tierra literalmente por el Ecuador, ¿qué tan más largo tendría que ser este larguísimo listón para "flotar" a 2cm de la tierra?
Tercero: este sitio web puede decirte en qué parte de la expansión decimal de π aparece la fecha de tu cumpleaños, si aparece. Escribe tu cumpleaños como MM/DD/AA porque así la escriben nuestros vecinos del norte. (Creo que puedes confiar en el sitio, es de Wolphram.)
Para leer más:
Luis Hernández Lamoneda, investigador del CIMAT, publicó en el Blog de Divulgación que CONACYT mantiene en El Universal, una entrada precisamente titulada Cuánto vale pi. Además, como es la leche, nos dejó publicarla en nuestro primer número de factorial!
Seguimos múltiples lecturas sobre la historia y las distintas demostraciones. Recomendamos en particular ésta de Mitch Rudominer porque nos parece completa y sencilla. También nos gustó mucho esta otra de Ilan Vardi. La historia la revisamos en esta entrada de David Wilson para un curso en Rutgers. Por último, ya habíamos discutido algunas cosas sobre π cuando hablamos de por qué no se puede cuadrar el círculo.
Algunas de nuestras fuentes fueron foros matemáticos en internet: acá vimos que la idea de que la razón del área entre el cuadrado del radio es constante sí está en Euclides, acá vimos muchas de nuestras fórmulas. Has visto que no nos da mucha pena usar la Wikipedia; tampoco los foros son malos mientras aprendas qué tomar y qué dejar. En particular, la demostración de por qué π es el mismo para cualquier círculo lo seguimos de acá.



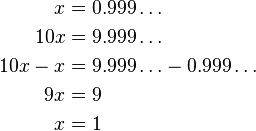
















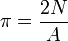

En el método de la pizza, ¿De dónde sale que la base, que si bien entiendo el porqué de que es media circunferencia, vale πr?
ResponderBorrarInvestigué un poco y me gustaría compartirlo: https://www.youtube.com/watch?v=DuxYZPtiz0s
ResponderBorrar¿ W.T.F ?
ResponderBorrarFue a las 20:57 no a las 18:57
BorrarHola :v
Borrar