Una ciudad llamada Königsberg
Una de las anécdotas y temas clásicos en la divulgación de matemática es la famosa ciudad de Königsberg, en la antigua Prusia, y sus siete puentes. La ciudad es ahora --y desde finales de la Segunda Guerra Mundial-- conocida como Kaliningrado y pertenece a Rusia --convirtiendo, además, al país ex soviético en una mancha no conexa--. Prusia llegó a ser un fuerte imperio y Königsberg una capital científica y cultural del mundo europeo a mediados del siglo XVIII que atraía grandes mentes de entonces, con renombrados científicos como miembros de su Academia Prusiana de las Ciencias (también conocida como Academia de Berlín).
Así es como se ve el centro de Kaliningrado actualmente, según la más reciente actualización de google maps y un par de siglos después de la época de la que estamos hablando:
Una de las anécdotas y temas clásicos en la divulgación de matemática es la famosa ciudad de Königsberg, en la antigua Prusia, y sus siete puentes. La ciudad es ahora --y desde finales de la Segunda Guerra Mundial-- conocida como Kaliningrado y pertenece a Rusia --convirtiendo, además, al país ex soviético en una mancha no conexa--. Prusia llegó a ser un fuerte imperio y Königsberg una capital científica y cultural del mundo europeo a mediados del siglo XVIII que atraía grandes mentes de entonces, con renombrados científicos como miembros de su Academia Prusiana de las Ciencias (también conocida como Academia de Berlín).
Así es como se ve el centro de Kaliningrado actualmente, según la más reciente actualización de google maps y un par de siglos después de la época de la que estamos hablando:
Como puedes observar, la ciudad de Königsberg, como muchas ciudades europeas, es atravesada por un río: el río Pregolya. Este río divide a la ciudad en dos orillas o riberas --la de acá y la de allá-- y rodea la isla de Kneiphof creando cuatro secciones separadas. Para unir los pedazos de ciudad existían --y existen, algunos remodelados-- siete puentes llamados del Herrero, Conector, Verde, del Mercado, de Madera, Alto y de la Miel. La ciudad fue bombardeada durante la segunda guerra mundial y destruyó dos de los puentes; además, al menos uno ha tenido que ser reconstruido para dar paso a carreteras modernas. Sin embargo, en la imagen de satélite todavía es posible apreciar los siete puentes, aunque en teoría son únicamente cinco ahora y solo dos de ellos estaba en pie en tiempos de Leonhard Euler, el querido protagonista de nuestra historia.
Como ocurría en prácticamente todo el mundo antes del internet y la televisión, la gente pasaba sus domingos paseando en familia por la ciudad. Para hacer el paseo más divertido, los habitantes se propusieron un juego: tratar de encontrar un camino que cruce todos y cada uno de los siete puentes una y solamente una vez y regrese al punto donde empezaron. En apariencia un problema sencillo y entretenido que la gente intentaba resolver por fuera bruta: intentando todos los caminos a ver si alguno funcionaba. El problema llegó a oídos de académicos y estudiantes y, eventualmente, hasta Euler, quien encontraría una manera de responder
Euler llegó a la Academia en 1744 siguiendo a su gran amigo Daniel Bernoulli desde San Petesburgo, donde trabajaban juntos. Había miembros muy destacados de la Academia en esos años, que vivía quizás su época de oro. En su solución al problema publicada en 1736, Euler veía Königsberg así:
Euler publicó su solución antes de irse a vivir a Prusia que, sí, le quita algo de magia a la anécdota porque no nos deja imaginar a Euler literalmente paseando por la ciudad mientras resuelve el problema, en un artículo titulado Solutio problematis ad geometriam situs pertinentis que puedes leer aquí en latín original -suponiendo que lees fluido latín. En la segunda página del documento aparece la imagen que incluimos arriba, junto a otra más complicada que busca ser general. Si estás familiarizado con el problema o su solución --o su página en Wikipedia-- debería sorprenderte no ver una imagen como la siguiente en ninguna página del artículo, sepas o no latín
y es que, pese a que el artículo de Euler se considera fundacional para la Teoría de Grafos, el matemático nunca usa las palabras "grafo", "gráfica" o nada parecido. La abstracción de Euler no incluyó publicar un dibujito del hoy famoso grafo de Königsberg, pero vamos por pedazos.
Euler explains it all
Primero: ¿cómo fue que Euler se enteró del problema? Fue gracias a una carta que le mandó su toyaco, Carl Leonhard Gottlieb Ehler, alcalde de Danzig --hoy Gdansk, en Polonia--, una pequeña ciudad a 80 kilómetros de Königsberg. Ehler y su amigo matemático Heinrich Kühn buscaban la solución al problema de los siete puentes y no habían tenido éxito. Así, el 9 de marzo de 1736, Ehler escribió a Euler pidiendo de la manera más humilde y encarecida que le hiciera paro con la tarea. En un principio, Euler no encontró el problema tan interesante y se lo hizo saber en su carta de respuesta del 3 de abril de 1737; sobre todo, le parecía muy alejado de las matemáticas y, por lo tanto, no entendía por qué necesitaban la ayuda de un matemático pues la solución se encontraba "a partir de razón y no de un principio matemático particular". Sin embargo, le parecía que podía pertenecer al área que Liebniz había descrito como geometría de la posición, aunque Euler mismo no tenía claro qué clase de problemas pertenecían a dicha área. (Quizás ni siquiera Liebniz mismo; se cree que podía hacer referencia a lo que hoy llamamos Topología.)
En una carta que Euler escribió a su amigo Giovanni Marinoni, matemático radicado en Vienna, el 13 de marzo de 1736, Euler describió el problema de los siete puentes como "banal", aunque le pareció interesante que ni la geometría, ni el álgebra, ni el conteo podían dar con la solución. Y así, procedió a describir la regla que le había permitido resolver el problema. En caso de que las fechas de las cartas sean las correctas, tenemos que suponer que tanto el servicio postal de la época como las habilidades de Euler para resolver problemas eran verdaderamente sorprendentes.
¿Cómo es la solución de Euler? Como ya vimos, su publicación no tiene dibujitos ni grafos por ningún lado. Lo que sí hace es nombrar las cuatro secciones como A, B, C, D como se ve en la figura que pusimos arriba. En su notación, escribir AB significa ir de la sección A la sección B, notando que es irrelevante cuál de los puentes se tome para cruzar. Luego, una cadena de n letras significa que ha cruzado n-1 puentes, de modo que para el problema de Königsberg se necesita una cadena de 8 letras. En su tabla, cuenta los puentes que van a cada una de las secciones y la "frecuencia", es decir, las veces que la letra debe aparecer en el código.
La regla de la frecuencia es como sigue: para una cantidad impar k de puentes que van a una sección, la letra debe aparecer (k+1)/2 veces. Esto es suficiente para el problema de Königsberg pues todas las secciones tienen una cantidad impar de puentes. Además, esto resuelve el problema pues si sumamos las frecuencias, las letras deben aparecer 3 + 2 + 2 + 2 = 9 veces, pero nuestro código debía tener únicamente 9 letras. Por lo tanto, es imposible.
Por supuesto, Euler no se detuvo ahí. Para una k par, el código debe incluir esa letra k/2 +1 veces si empieza en dicha sección, k/2 veces si no. Con esta información se dispuso a atacar el problema general. Observa que la suma de los números en su primera columna --la de los puentes que conectan cada sección-- debe ser igual al doble de puentes en el problema, pues aparece una vez por cada sección que conecta. (En el camino, Euler resolvió un viejo problema, el de los apretones de mano.)
Las conclusiones de Euler son tres:
Para trabajar en casa:
Cuando yo estudié la primaria tampoco teníamos internet en los celulares --la culebrita del Nokia no nos llegaría hasta la secundaria-- así que encontrábamos otras maneras de divertirnos. El problema consiste en dibujar una casita sin levantar el lápiz ni cruzar la misma línea dos veces
El problema es originalmente un acertijo alemán para niños llamado "la casa de Santa Claus" pues los niños debían decir una sílaba de la frase Das ist das Haus des Nikolaus, esta es la casa de Santa Claus (o, la terrible versión para niñas, Wer dies nicht kann, kriegt keinen Mann, quien no pueda hacer este dibujo no conseguirá un hombre).
No es posible empezar y terminar en el mismo punto, es decir, no es posible construir un paseo euleriano. Sin embargo, sí es posible dibujar la casita, por ejemplo
En total hay 88 soluciones distintas, que no son paseos eulerianos. En este enlace hay una presentación de PowerPoint con un .gif que anima 44 de ellas --las otras 44 son simétricas, desde el otro punto-- porque no pude encontrar la animación de nuevo.
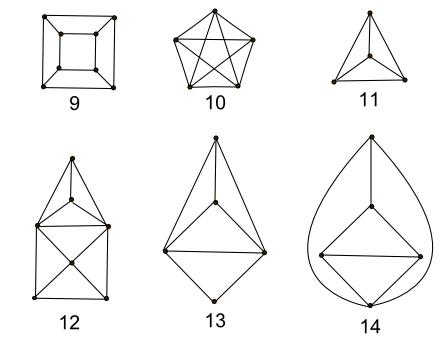
El punto es que hay muchos acertijos similares que puedes hacer --o ponerle a tus alumnos para pasar el rato y que intenten llegar a los teoremas de Euler por su cuenta-- como los siguientes:
Hemos recopilado --que es una palabra bonita para "robar"-- algunos para tener una página completa de ellas que puedes encontrar acá en una versión para imprimir.
Referencias y lecturas:
Durante gran parte del artículo, seguimos las investigaciones de Hopkins y Wilson en un artículo titulado The truth about Königsberg. Incluye traducciones del original.
Existe una traducción al inglés del artículo original de Euler en Graph Theory 1736-1936 de Biggs, N. L.; Lloyd, E. K.; y Wilson, R. J. No hemos podido conseguir un enlace. Pero te recordamos el original Geometriam Sitius y te recordamos que google translate incluye latín.
Las entradas sobre el problema de los siete puentes en MathWorld de Wolfram y, por supuesto, en la Wikipedia.
Un trabajo escolar --College of New Jersey-- que aborda el problema desde la perspectiva histórica, de Teo Paoletti. Incluye algunas traducciones del original.
Como ocurría en prácticamente todo el mundo antes del internet y la televisión, la gente pasaba sus domingos paseando en familia por la ciudad. Para hacer el paseo más divertido, los habitantes se propusieron un juego: tratar de encontrar un camino que cruce todos y cada uno de los siete puentes una y solamente una vez y regrese al punto donde empezaron. En apariencia un problema sencillo y entretenido que la gente intentaba resolver por fuera bruta: intentando todos los caminos a ver si alguno funcionaba. El problema llegó a oídos de académicos y estudiantes y, eventualmente, hasta Euler, quien encontraría una manera de responder
Euler llegó a la Academia en 1744 siguiendo a su gran amigo Daniel Bernoulli desde San Petesburgo, donde trabajaban juntos. Había miembros muy destacados de la Academia en esos años, que vivía quizás su época de oro. En su solución al problema publicada en 1736, Euler veía Königsberg así:
Euler publicó su solución antes de irse a vivir a Prusia que, sí, le quita algo de magia a la anécdota porque no nos deja imaginar a Euler literalmente paseando por la ciudad mientras resuelve el problema, en un artículo titulado Solutio problematis ad geometriam situs pertinentis que puedes leer aquí en latín original -suponiendo que lees fluido latín. En la segunda página del documento aparece la imagen que incluimos arriba, junto a otra más complicada que busca ser general. Si estás familiarizado con el problema o su solución --o su página en Wikipedia-- debería sorprenderte no ver una imagen como la siguiente en ninguna página del artículo, sepas o no latín
y es que, pese a que el artículo de Euler se considera fundacional para la Teoría de Grafos, el matemático nunca usa las palabras "grafo", "gráfica" o nada parecido. La abstracción de Euler no incluyó publicar un dibujito del hoy famoso grafo de Königsberg, pero vamos por pedazos.
Euler explains it all
Primero: ¿cómo fue que Euler se enteró del problema? Fue gracias a una carta que le mandó su toyaco, Carl Leonhard Gottlieb Ehler, alcalde de Danzig --hoy Gdansk, en Polonia--, una pequeña ciudad a 80 kilómetros de Königsberg. Ehler y su amigo matemático Heinrich Kühn buscaban la solución al problema de los siete puentes y no habían tenido éxito. Así, el 9 de marzo de 1736, Ehler escribió a Euler pidiendo de la manera más humilde y encarecida que le hiciera paro con la tarea. En un principio, Euler no encontró el problema tan interesante y se lo hizo saber en su carta de respuesta del 3 de abril de 1737; sobre todo, le parecía muy alejado de las matemáticas y, por lo tanto, no entendía por qué necesitaban la ayuda de un matemático pues la solución se encontraba "a partir de razón y no de un principio matemático particular". Sin embargo, le parecía que podía pertenecer al área que Liebniz había descrito como geometría de la posición, aunque Euler mismo no tenía claro qué clase de problemas pertenecían a dicha área. (Quizás ni siquiera Liebniz mismo; se cree que podía hacer referencia a lo que hoy llamamos Topología.)
 |
| Topología |
En una carta que Euler escribió a su amigo Giovanni Marinoni, matemático radicado en Vienna, el 13 de marzo de 1736, Euler describió el problema de los siete puentes como "banal", aunque le pareció interesante que ni la geometría, ni el álgebra, ni el conteo podían dar con la solución. Y así, procedió a describir la regla que le había permitido resolver el problema. En caso de que las fechas de las cartas sean las correctas, tenemos que suponer que tanto el servicio postal de la época como las habilidades de Euler para resolver problemas eran verdaderamente sorprendentes.
¿Cómo es la solución de Euler? Como ya vimos, su publicación no tiene dibujitos ni grafos por ningún lado. Lo que sí hace es nombrar las cuatro secciones como A, B, C, D como se ve en la figura que pusimos arriba. En su notación, escribir AB significa ir de la sección A la sección B, notando que es irrelevante cuál de los puentes se tome para cruzar. Luego, una cadena de n letras significa que ha cruzado n-1 puentes, de modo que para el problema de Königsberg se necesita una cadena de 8 letras. En su tabla, cuenta los puentes que van a cada una de las secciones y la "frecuencia", es decir, las veces que la letra debe aparecer en el código.
La regla de la frecuencia es como sigue: para una cantidad impar k de puentes que van a una sección, la letra debe aparecer (k+1)/2 veces. Esto es suficiente para el problema de Königsberg pues todas las secciones tienen una cantidad impar de puentes. Además, esto resuelve el problema pues si sumamos las frecuencias, las letras deben aparecer 3 + 2 + 2 + 2 = 9 veces, pero nuestro código debía tener únicamente 9 letras. Por lo tanto, es imposible.
Por supuesto, Euler no se detuvo ahí. Para una k par, el código debe incluir esa letra k/2 +1 veces si empieza en dicha sección, k/2 veces si no. Con esta información se dispuso a atacar el problema general. Observa que la suma de los números en su primera columna --la de los puentes que conectan cada sección-- debe ser igual al doble de puentes en el problema, pues aparece una vez por cada sección que conecta. (En el camino, Euler resolvió un viejo problema, el de los apretones de mano.)
Las conclusiones de Euler son tres:
- Si hay más de dos regiones con una cantidad impar de puentes, el paseo es imposible.
- Si el número de puentes es impar para exactamente dos regiones, el paseo es posible si empieza en una de estas dos.
- Si todas las regiones tienen una cantidad par de puentes, entonces el paseo es posible empezando en cualquiera de éstas.
 |
| Inclina la cabeza a la izquierda |
Para trabajar en casa:
Cuando yo estudié la primaria tampoco teníamos internet en los celulares --la culebrita del Nokia no nos llegaría hasta la secundaria-- así que encontrábamos otras maneras de divertirnos. El problema consiste en dibujar una casita sin levantar el lápiz ni cruzar la misma línea dos veces
El problema es originalmente un acertijo alemán para niños llamado "la casa de Santa Claus" pues los niños debían decir una sílaba de la frase Das ist das Haus des Nikolaus, esta es la casa de Santa Claus (o, la terrible versión para niñas, Wer dies nicht kann, kriegt keinen Mann, quien no pueda hacer este dibujo no conseguirá un hombre).
No es posible empezar y terminar en el mismo punto, es decir, no es posible construir un paseo euleriano. Sin embargo, sí es posible dibujar la casita, por ejemplo
En total hay 88 soluciones distintas, que no son paseos eulerianos. En este enlace hay una presentación de PowerPoint con un .gif que anima 44 de ellas --las otras 44 son simétricas, desde el otro punto-- porque no pude encontrar la animación de nuevo.
El punto es que hay muchos acertijos similares que puedes hacer --o ponerle a tus alumnos para pasar el rato y que intenten llegar a los teoremas de Euler por su cuenta-- como los siguientes:
Referencias y lecturas:
Durante gran parte del artículo, seguimos las investigaciones de Hopkins y Wilson en un artículo titulado The truth about Königsberg. Incluye traducciones del original.
Existe una traducción al inglés del artículo original de Euler en Graph Theory 1736-1936 de Biggs, N. L.; Lloyd, E. K.; y Wilson, R. J. No hemos podido conseguir un enlace. Pero te recordamos el original Geometriam Sitius y te recordamos que google translate incluye latín.
Las entradas sobre el problema de los siete puentes en MathWorld de Wolfram y, por supuesto, en la Wikipedia.
Un trabajo escolar --College of New Jersey-- que aborda el problema desde la perspectiva histórica, de Teo Paoletti. Incluye algunas traducciones del original.






No hay comentarios.:
Publicar un comentario